Chapitre 5
Analyse de distorsion aléatoire

retour vers la table des matières

5.1 Introduction
Dans ce chapitre nous voulons examiner le comportement, au niveau de la distorsion, d'une chaîne de transmission FM, émettant un signal composite stérdo avec EMCS, dont tous les signaux modulants sont du type aléatoire. Nous pensons que l'emploi de signaux aléatoires se justifie par le fait qu'ils constituent un meilleur modèle que les signaux harmoniques pour représenter des signaux réels tels la musique ou la parole. L'emploi de signaux aléatoires ne nous permet plus d'utiliser la FFT. On doit donc faire appel à des méthodes analytiques assez complexes, qui limitent rapidement la portée de cette approche. Par conséquent, on utilisera le modèle simple de la figure 3.12, et les résultats porteront uniquement sur le signal composite, et non plus sur le signal modulant EMCS comme dans l'analyse harmonique. De plus, les résultats ne vaudront que pour un filtre trés simple du type Butterworth ordre 1. Cette contrainte est due à= l'emploi d'une méthode de calcul particulière en l'occurrence celle de Bedrosian & Rice (4). De plus, cette méthode exige le caractére gaussien du signal composite et, comme on le sait, le pilote et le signal FM-EMCS ne remplissent pas cette dernière exigence. Malgré ce la, il demeure intéressant d'examiner ce qu'on a pu obtenir d'une telle méthode.

5.2 Développement mathèmatique
On utilisera le modèle de la figure 3.12. Pour pouvoir traiter le problème pour le cas où le signal composite est un signal aléatoire, il faut trouver une relation liant la densité spectrale de la phase à la sortie, à la densité spectrale de la phase à l'entrée:

où est le signal composite à l'entrée du modulateur de phase, tandis que e est le signal composite à la sortie du démodulateur de phase.

La relation liant les densités spectrales des fréquences instantanées à l'entrée et à la sortie s'obtient aisément de la première relation car:

Le développement de Bedrosian & Rice (4) se résume à:

1) Trouver une relation temporelle liant à .
2) Développer en série de Taylor cette relation.
3) Passer dans le dommaine spectral pour le cas où le signal composite est gaussien.

Le développement en série permet de pouvoir distinguer à la sortie le premier terme de la série comme le signal utile, et les autres termes comme de la distorsion. Pour le cas harmonique, un développement en série n'est pas nécessaire car la distorsion s'identifie immédiatement dans le dommaine spectral. Par contre, les spectres de signaux aléatoires sont en général oontinus et la distorsion ne se distingue plus aussi clairement. Le développement en série permet donc de pouvoir sqparer le signal utile du signal de distorsion.

Sans présenter toutes les étapes, on obtient la relation temporelle suivante:

où Y(t) est la représentation en bande de base du filtre de canal passe-bande. Pour le cas où F(t) est réel, on obtient le développement en série suivant:

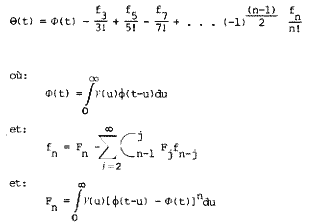
Il suffit maintenent de calculer:

Nous allons le faire en supposant que est un processus aléatoire gaussien stationnaire. Dans le calcul de ^W on obtient trois types de termes:

1) Terme linéaire noté que l'on appellera signal utile
2) Termes croisés notés que l'on pourrait appeler distorsion correlée

3) Termes non linéaires notés que l'on appelera distorsion d'intermodulation

Dans le développement en série, nous ne retenons que le terme d'ordre trois, ce qui implique que l'on prend:

alors:

Le premier terme (le terme linéaire) s'obtient aisément; c'est la sortie d'un filtre linéaire:

Pour les deux autres termes, il faut calculer les moments d'ordre plus élevés d'une variable aléatoire gaussienne. On peut le faire à l'aide de la fonction caractéristique suivante:

où A(w) est la réponse en fréquence d'un cpérateur linéaire L(). On obtient pour

Et pour on a:

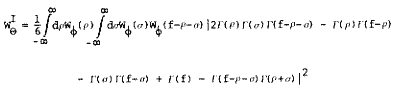
5.3 Résultats des calculs
Il suffit maintenent d'évaluer ces trois expressions et remplacer par la densité spectrale du signal oomposite et rt f) par la réponse en fréquence d'un filtre donné.

Les calculs ont été réalisés pour un signal oomposite standard dont chaque composante possède une densité spectrale blanche. Pour l'EMCS . cependant, une densité spectrale de forme gaussienne a aussi été utilisée, cette forme de densité pour l'EMCS, nous le pensons, étant plus prés de la réalité. En effet, d'aprés (5), on sait que le spectre d'un signal FM à haut indice de modulation, modulé par un signal aléatoire, aura la forme de la densité de probabilité du signal modulant. Comme le signal modulant possède une distribution gaussienne, la forme du spectre devrait avoir une allure gaussienne. Toutefois, comme l'indice de modulation n'est pas très élevé en pratique, on serait probablement dans un cas intermédiaire.

5.3.1 Calculs des densités spectrales
Nous présentons aux figures 5.1 à 5.11 les résultats du calcul des trois densités pour le cas d'un filtre d'ordre 1 de la forme:

Les pondérations de chaque composante spectrale ont été déterminées dans (1) pour le cas d'un signal composite aléatoire et constituent des pondérations standards. On a donc pour chaque composante:

G+D : 62.7%
G-D : 31.3%
Pilote : 3%
EMCS : 3%

On a réalisé les calculs pour trois conditions différentes d'opération du systéme:

A Toutes les composantes sont présentes
B Canal EMCS absent
C Modulation stéréophonique absente (pilote seulement)

Pour chacune de ce s conditions, trois valeurs du paramètre B/FC ont été utilisées. Ce paramètre est une mesure de la largeur du canal. En effet avec B=15 kHz, on peut calculer la largeur du canal W à partir de B/FC comme suit:

On obtient pour les trois valeurs de B/FC choisies:

L'ensemble des conditions d'expérimentations sont présenté au tableau 5.3.1. Plusieurs remarques peuvent être faites à partir de ces quelques courbes.

La distorsion linéaire causée par le filtre et présente dans est à peu prés imperceptible pour les cas étudiés. Donc constitue bien une bonne approximation du signal utile.

La densité spectrale occupe la méme bande que comme on s'y attendait, puisque celui-ci possède le signal utile comme facteur multiplicatif. Etant donné le niveau relativement élevé de on pourrait penser à additionner celui-ci à pour constituer le signal utile. Toutefois dans les calculs de S/D, cela ne ferait que peu de différences.

La densité spectrale , quant à elle, occupe toute la bande et méme au-delà. Sa forme est généralement continue mais peut devenir un peu bizarre, dépendant des cas comme celui où la modulation stérdo est absente et où seulement le pilote et l'EMCS sont transmis (voir figures 5.3, 5.6, 5.9 et 5.11). Ceci est principalement dû à l'utilisation d'un nombre de termes trés limité dans le calcul de la série. De plus, en absence de modulation stéréophonique, on pourrait mettre en doute la validité du caractére gaussien du signal composite. Pour cela, nous n'accorderons pas trop d'importance à ce cas particulier.

L'allure de la densité spectrale d'intermodulation ne change pas beaucoup en fonction de la forme du spectre EMCS (voir figures 5.1 et 5.10). Ce qu'on peut déduire de cela, c'est que l'allure du spectre EMCS n'aura pas d'influence significative sur le S/D avant démodulation. Rien ne permet de dire cependant, qu'il en serait de méme pour le S/D après démodulation, si celui-ci était disponible.

Les niveaux de et diminuent à mesure que l'on élargit le filtre de canal et demeurent relativement élevés même pour des largeurs allant jusqu'à 600 kHz. Ceci est probablement dû à l'emploi d'un filtre d'ordre trés faible.

On remarque que le niveau de distorsion est à peu prés constant dans toute la bande du signal composite. Cela semble nous indiquer des performances au niveau de l'EMCS au moins égales à celles des autresh canaux. Ce qui semble un peu surprenant.

On note aussi la faible contribution au niveau de la distorsiont apportée par le canal EMCS. Il suffit de comparer les figures 5.1 et 5.2. La grande part de la distorsion provient en fait du canal stéréo.

5.3.2 Calcul de S/D
Pour mesurer la distorsion introduite par un système, on a souvent recours en pratique à un signal-test aléatoire. Ce genre de signal se rapproche davantage des caractéristiques d'un signal réel, mais il a ses désavantages. Comme la densité spectrale d'un tel signal n'est pas de nature discrète mais continue, il devient impossible de distinguer distorsion du signal utile à la sortie. Pour résoudre ce problème, on utilise comme signal test, un bruit blanc dans lequel le spectre contient une fente étroite. Cette fente doit en principe être la plus étroitc possible et être située au point de la bande où on veut mesurer la valeur de la densité spectrale d'intermodulation. Il suffit de mesurer alors la puissance à l'intérieur de cette fente étroite. Dans l'approche analytique utilisée on obtient trois types de termes distincts: la densité spectrale linéaire, la densité spectrale croisée et la densité spectrale d'intermodulation. Chaque densité a la forme suivante:

Seul est considéré vraiment de la distorsion, car c'est le seule terme parmi les deux termes contenant de la distorsion non linéaire que l'on peut mesurer. pourrait être visualisé à l'aide de l'exemple suivant:

Si on a à la sortie du systéma y(t) = stt) + d(t) où s(t) est le signal utile et d(t) la distorsion, le calcul de G_y(f) donnera:

G_y(f) = [Y(f) x Y(-f)] = [S(f) + D(f)] x [S(-f) + D(-f)]
G_y(f) = G_s(f) + G_d(f) + 2Re [S(f) x D( f)]

où G_s(f) correspond à , G_d(f) à et le dernier terma à . Ce dernier terma représenterait donc comme une masure de la corrélation entre les signaux s(t) et d(t). Dans le cas harmonique, est toujours nul car des signaux harmoniques sont orthogonaux entre eux. Que doit-on faire avec le terme croisé ? En fait plus la relation entre s(t) et d(t) est forte, plus sera grand. Donc pour être plus précision pourrait faire la chose suivante:

est grand, on l'ajoute à

est faible, on l'ajoute à

On pourrait dans plusieurs cas tout aussi bien laisser tomber ce terme sans causer d'erreurs importantes: on le fera d'ailleurs dans les calculs qui vont suivre.

Donc pour calculer S/D, il suffit de calculer l'expression suivante:

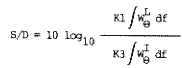
Ce qui nous intéressera dans cette section sera de calculer S/D dans b le canal EMCS. On devra donc calculer les intégrales de la définition qui précède avec comme bornes d'intégration la largeur allouée au canal EMCS, avec les paramètres K1 et K3 déterminés comme suit:

K1 = D² /fc

et

avec D = 75 kHz

Notons que le S/D calculé ici porte sur le signal EMCS modulé. Le calcul du dénominateur a été réalisé de deux façons différentes:

1) EMCS absent
2) EMCS présent

La première condition se rapproche davantage des tests réalisés en laboratoire avec des signaux aléatoires. Notons finalement que les calculs de S/D qui suivent ont été faits pour un spectre EMCS blanc. Cette dernière forme permet une plus grande rapidité des calculs. De toute manière, on a vu précédemment que la forme du spectre avait peu d'influence sur le niveau de distorsion et par conséquent on peut s'attendre à peu de différences dans les calculs de S/D pour différentes formes de spectre EMCS.

Les résultats obtenus pour les deux conditions discuté~s et pour deux valeurs de pondération de l'EMCS sont présentés en fonction de B/F: et PC aux tableaux 5.3.2 à 5.3.5. Dans l'ensemble, les niveaux de S/D sont= relativement faibles. Ceci pourrait s'expliquer par l'utilisation d'un= filtre de canal d'ordre 1. Une augmentation trés importante pourrait être obtenue par l'emploi d'un filtre d'ordre plus élevé. De plus, comme an le sait, ces valeurs portent sur un signal FM modulé, ce qui permet d'attendre une augmentation additionnelle du S/D aprés démodulation, proportionnelle au carré de l'indice de modulation de la porteuse EMCS. Si on examine les valeurs de S/D obtenues en fonction de PC, an remarque le peu d'améliorations qu'apporte le déplacement du canal EMCS vers les fréquences supérieures. Le gain faible qu'an obtient dans certains cas serait rapidement compensé par une augmentation du rapport signal sur bruit résultant de la diminution de l'indice de modulation de la porteuse principale.

On note une augmentation d'environ 4 dB sur l'ensemble des valeurs de S/D lorsque l'an passe de 3% à 10% pour la pondération de l'EMKS. Cette augmentation correspond presque uniquement à l'augmentation de la puissance-du signal linéaire, puisque le signal de distorsion n'est pas beaucoup affecté par des partitions substantielles des composantes du signal composite. Danc le seul avantage qu'an aurait à augmenter la puissance de l'EMCS, serait en vue de l'amélioration du rapport signal sur bruit dans le canal EMCS qui, an le sait, est désavantagé du fait de sa situation dans les hautes fréquences dans la bande de base.

B/FC	PC (kHz)
	67	76	85	95
.05 .075 .10	35.7 25.7 18.4	35.9 25.8 18.8	36.0 26.0 19.1	36.4 26.5 19 8

Tableau 5.3.2 EMCS présent
Pondération: 3%

B/FC	PC (kHz)
	67	76	85	95
.05 .075 .10	35.7 26.7 19.3	35.9 25.8 18.8	36.0 26.0 19.1	36.4 26.5 19 8

Tableau 5.3.3 EMCS absent
Pondération: 3%

B/FC	PC (kHz)
	67	76	85	95
.05 .075 .10	40.0 29.9 22.9	39.8 29.8 22.9	39.5 29.6 22.9	39.3 29.5 23.1

Tableau 5.3.4 EMCS présent
Pondération: 10%

B/FC	PC (kHz)
	67	76	85	95
.05 .075 .10	42.9 32.7 25.5	43.5 33.3 26 2	44.0 33.8 26.8	45.2 35.0 20.1

Tableau 5.3.5 EMCS absent
Pondération: 10%

5.4 Problémas rencontrés dans les calculs
Le travail a consisté à calculer et , puisque ne pose aucune difficulté. On a une intégrale simple à résoudre pour et une intégrale double pour We . Plusieurs méthodes numériques sont disponibles, mais celle retenue fut la méthode ittérative de Ramberg, car elle permet de contrôler la précision des résultats. Il est évidant que pour avoir des temps de calcul raisonnables, on devra se contenter d'une précision faible mais suffisante. La première approche utilisée dans la programmation des expressions numériques, fut d'utiliser la forme générale et de faire les calculs en nombres complexes. Cela implique que l'on utilise une sous-routine pour calculer la fonction de transfert du filtre puis on calcule l'intégrant en faisant appel à des opérations d'arithmétique complexes. Les conséquences immédiates sont la lenteur des calculs et la faible précision obtenue, surtout lors du calcul de . Ceci est compréhensible puisque pour chaque valeur de , on doit évaluer la fonction à intégrer plusieurs milliers de fois. Donc, on a avantage à simplifier au maximum cette fonction. Ceci se réalise en remarquant le fait que le résultat final du calcul doit être réel étant donné que l'a,n calcule des densités spectrales. Il suffit donc de simplifier, pour un filtre donné, la fonction à intégrer en une fonction réelle dont l'arithmétique réelle est plus rapide. La tâche exigée pour simplifier ces expressions estanorme et n'a pu être réalisoe que pour un filtre trés simple tel un filtre Butterworth d'ordre 1. Méme en utilisant un traitement d'équations par ordinateur, on n'arrive pas à faire la simplification pour un autre type de filtre car les temps de traitement deviennent vite trop longs. Il y aurait lieu, si le temps nous le permettait, d'essayer de trouver une méthode efficace afin de rendre la simplification une tâche possible pour tout types de filtres. Il serait intéressant de voir les résultats qu'an obtiendraient si on utilisait d'autres types de filtres. Cela pourrait fournir des résultats bien différents de ceux obtenus présentement. Il serait désirable aussi de pouvoir ajouter quelques termas de plus à la série, mais, an s'en doute, les temps de calculs qu'on obtiendraient avec les moyens dont on dispose présentement, ne nous permet pas d'y penser trop. Un résumé de ce qui vient d'être dit est présenté au tableau 5.4.1.

5.5 Conclusion
Les résultats de quelques expériences simples ont été présentés dans cette dernière partie dont l'analyse est basée sur des signaux aléatoires. La complexité des calculs ne nous permet pas de faire tout ce qu'on voudrait.

Des densités spectrales ont été tracées pour différents cas simples et quelques valeurs du paramètres B/FC. L'observation de ce s densités spectrales nous a permis de constater, dans les conditions présentes, la faible influence de l'EMCS sur le niveau de distorsion et, par conséquent, sur la qualité de la stérdophonie. La majorité de la puissance du signal de distorsion provient en fait du canal stéréo. On a pu constater le peu de changements que pourraient apporter différentes formes du spectre pour le canal EMCS, sur le niveau de distorsion et, par conséquent, sur la qualité de l'EMCS avant démodulation.

Des calculs de S/D ont été présentés pour différentes valeurs de B/F:, FC et P3. Ces résultats nous ont permis d'observer le peu d'avantage que pourrait apporter pour l'EMCS, le déplacement de sa sous-porteuse vers des fréquences supérieures. Ils nous ont permis également de réaliser que l'augmentation du S/D dans le canal EMCS, résultant de l'augmentation de la puissance de ce dernier, ne faisait qu'augmenter la puissance du signal linéaire et à peu prés pas la distorsion à la sortie.

L'approche utilisée ici ne nous permet pas de pousser l'étude beaucoup plus loin, quand on considére les temps de calculs. Plusieurs obstacles, comme l'utilisation de filtres d'ordre plus élevé et la démodulation du canal EMCS ne sont pas encore franchis, mais pourraient fournir des renseignements intéressants si on s'y attardait.

On pourrait se poser quelques questions en rapport avec la validité du développement analytique, qui exige le caractére gaussien et stationnaire du signal composite. Deux composantes ne rencontrent pas ces exigences: ce sont le pilote et le canal EMCS lui-même. Pour le pilote, on a affaire à un signal non aléatoire, tandis que que pour l'EMCS, on a un signal FM modulé par un signal aléatoire. Dans ce cas, même si l'allure du spectre est gaussienne, la distribution de probabilité du signal FM ne sera certainement pas gausienne. Toutefois, vu la faible pondération de ces deux composantes, le signal composite peut être considéré quasi-gaussien, et les résultats valides.

Figures

5.1 Toutes les composantes sont présentes, B/FC=0.1

5.2 Canal EMCS absent, B/FC=0.1

5.3 Modulation stéréophonique absente, B/FC=0.1

5.4 Toutes les composantes sont présentes, B/FC=0.075

5.5 Canal EMCS absent, B/FC=0.075

5.6 Modulation stéréophonique absente, B/FC=0.075

5.7 Toutes les composantes sont présentes, B/FC=0.05

5.8 Canal EMCS absent, B/FC=0.05

5.9 Modulation stéréophonique, B/FC=0.05

5.10 Toutes les composantes sont présentes, B/FC=0.10 Spectre EMCS gaussien

5.11 Modulation stéréophonique absente, B/FC=0.10 Spectre EMCS gaussien